深入學習 lsd-slam - 3
前言
在 深入學習 LSD-SLAM - 2 裡面,我們簡單介紹了 Direct Method,先初步地了解這個方法的大致意義,今天再讓我們更深入一點,開始跟 paper 的內容銜接,之後會慢慢越來越深入好玩!
Spiral learning
因為這次剛好也是我第一次真正來學 SLAM 相關技術,以前都只是大略看看,沒有真正學通的感覺,所以也想跟大家分享一下個人學習的心得。
大家或多或少應該都經歷過一個情境 - 你要學習一個東西,但是因為這個東西並不是你熟悉的,所以你很容易在還沒學通前就卡住。但是隨著你用各種方法(例如:找不同的資料、上論壇發問、找厲害的朋友問、自己慢慢沉思等等),你會在某個時刻突然通某些原本不通的點。
啊為什麼要說這件事呢?
因為如果你可以看得到自己是怎麼學習的,你才有機會優化自己的學習方法,或至少能更好地安排時間來學習困難的技術。我們的學習過程往往不會是一直線,因為你一開始就是不會,才需要學,那又怎可能容易讓你一帆風順地從不會學到會。就算修課,老師已經盡量將課程內容整理清楚,也不一定完全適用於你的學習,所以你還是需要作一些額外的變通來幫助自己真正學通。
有人把這種學習的過程稱作 Spiral learning,Google 一下就可以看到很多 相關的資料。
像我自己目前就比較喜歡用時間來沉澱,然後在適當的時機再次學習,往往就能達到更好的效果,這樣的習慣在面對真正困難的題目的時候,比較容易有機會學通。雖然代價是更長的時間,不過只要願意優化,總是有機會再找出優化學習法的機會。我覺得有一篇文章 - 《時間與節奏的力量》把我想說的概念用另一種方式很清楚地再說一次,推薦給想要解決困難問題的朋友!
接下來我們先切回正題,隨著這個系列文的進展,我們會一起越來越深入 LSD SLAM!
再訪 Direct Method
一般來說,我們要學習一個東西,需要先抓到他的主要概念。像是 Direct method,我們總是要先見林,比較知道怎麼看裡面的樹。如果你有點忘記上次說了什麼,可以 回去翻翻。
首先,我們先回憶一下,現在的目的是什麼;
- 是要定位相機 pose,並同時定位
- 為達目的,這邊需要用影像資訊來估計 pose
- 為了估計 pose,需要計算 photometric error
然後,我們就接到論文中的這個公式了:
裡面的 $i$ 就是指 pixel 的 index,也就是說,這個公式是已知 $\xi$ (兩張影像之間的相機 pose 轉換),要計算在這個 $\xi$ 下,所有兩張影像中兩兩對應的 pixel 值相減完的總和,可以想像成是殘餘的誤差(residual)。對第 $i$ 個 pixel 來說,殘餘誤差就是 $ r_i(\xi) $,所以 $E(\xi)$ 就是所有殘餘誤差平方的總和。
$\xi$、$\omega$ 是什麼?
雖然我們現在大致上知道上面公式的意義,但是眼尖的讀者會發現裡面有一些不明的定義,例如 $\xi$ 以及 $\omega$。首先讓我們翻翻論文,他前面就有先提到這兩者:
很顯然,因為 $\omega$ 裡面需要用到 $\xi$,所以應該先了解他,再來了解 $\omega$。在這邊,我們暫且先把 $\xi$ 想成是 $G$,是一種 transform。然後 $\omega$ 是一種 warping,對深度為 $d$ 的點 $p$ 進行 $\xi$ 的 transform。
再度深入 $\xi$
上一個小段落裡,我們知道 $\xi$ 大概是跟 $G$ 有點關係,但是關係還不明確,只有一個糊糊的概念,現在就讓我們來理清楚。
3D Rigid body transform
要弄清楚 $G$ 跟 $\omega$ 的關係,我們要先弄懂 $G$ 跟 $\omega$ 分別是什麼,然後才能看關係。所以我們從比較簡單的 $G$ 開始。
$G$ 就是一個可以對三維世界中的任意一點 $x$,做一個操作,使得 $x$ 點被轉換到 $x^\prime$:
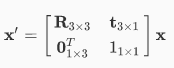
從 這個網頁 可以看到對一群點做一樣的 transform 的效果。
李群與李代數
好,上面講的這個 transform 我們已經懂了,下一個問題就是,$SO(3)$ 跟 $\mathfrak{se}(3)$ 又是什麼東西呢?以下我們依次簡介:
群:同一種東西的集合再加上同一種運算所構成的結構。記成 $(A,\cdot)$,要注意的是, $\cdot$ 運算需要滿足幾個條件,其中一個是封閉性:
$$\forall a_1, a_2, \quad a_1 \cdot a_2 \in A$$
剩下的我們等有需要再提。
$SO(n)$:特殊正交群,也就是 $n$ 維空間上的旋轉矩陣構成的群。所以你可以想像,你手上有一群 $n \times n$ 的矩陣,每個都符合下式中旋轉矩陣的特性,那這一群矩陣,跟這群矩陣可以做的運算就構成了 $SO(n)$。
$\begin{equation} SO(n) = { \mathbf{R} \in \mathbb{R}^{n \times n} | \mathbf{R R}^T = \mathbf{I}, det(\mathbf{R})=1 } \end{equation}$
$SE(n)$:概念上在 $SO(n)$ 的旋轉矩陣上加上一個平移向量。例如 $SE(3)$ 的定義如下。
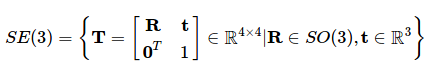
- $\mathfrak{so}(3)$ 跟 $\mathfrak{se}(3)$:李代數,他的定義是在單位矩陣處的正切空間(tangent space),這很難簡單敘述,建議有興趣的讀者可以去看看 這篇文章,之後有需要我再仔細描述。
所以!綜合以上所述,你會知道原來 $G$ 就是 $SE(3)$ 這種群,可以對三維空間中的點做旋轉和平移。然後,$\xi$ 是 $\mathfrak{se}(3)$ ,就是被定義在 $SE(3)$ 單位矩陣位置的 tangent space。
你可能想問,我們明明直接使用 transform,然後想辦法計算出 $E(\xi)$ 就好了,何必用到什麼李群或是李代數呢?
其實,問題就在於,我們想要優化的 transform 有 6 個變數,你想要有效率地優化有 6 自由度的東西,就會需要算導數(之後會引出 Jacobian 矩陣),且因為我們想要優化的目標還具備一些數學上的特性,如果能對他掌握得更好,我們就能更有效率地解決最佳化問題。
我現在的理解只夠說出這樣的解釋,不過隨著之後的系列往下看,我們會更能發掘引進李代數的美妙之處。
再訪 $\omega$
所以,到這邊我們可以對 $\omega$ 更加了解,他其實就只是一個運算,因為 $\xi$ 僅僅定義了這個 transform,但是沒有定義該怎麼對一個點操作。這也是為什麼我們需要 $\omega$。
前面提過,$\omega$ 是一種 warping,對深度為 $d$ 的點 $p$ 進行 $\xi$ 的 transform。之所以要定義深度 $d$,是因為 $p$ 只是一個二維平面上的一點,當然在這篇論文中指的就是影像上的一個 pixel。但是 $\omega \in se(3)$ 顯然需要對三維空間中的一點操作,所以需要 $d$ 的資訊。
總結
這次開始從一個比較 rough 的概念,深入到一點點論文中的細節了。我希望把這系列定位成真正了解論文的一個系列,所以對於有相關基礎的讀者來說可能覺得過程寫得太簡單。不過,網路上太多寫得不清楚的資源了,對基礎不夠的人學起來應該頗痛苦(像我就是),所以還是希望可以提供一個比較完整的系列,也嘗試在裡面使用 spiral learning 的技巧不斷重訪某些觀念、不斷深入。
隨著我們慢慢地進展,我們準備可以把優化 $E(\xi)$ 的各項細節都好好地來通達一下,我們下回再見!
延伸閱讀
- LSD-SLAM深入學習(2)-算法解析
- 視覺 SLAM 中的數學基礎 第一篇 3D 空間的位置表示
- lie group and computer vision : 李群、李代數在計算機視覺中的應用
- Multiple View Geometry - Lecture 3 (Prof. Daniel Cremers)
關於作者:
@pojenlai 演算法工程師,對機器人跟電腦視覺有少許研究,最近在鍛鍊自己的執行力

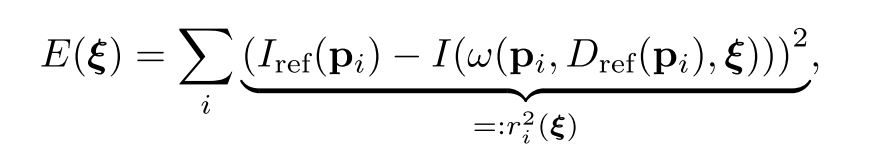


留言討論