前言

學習電腦視覺的同學們應該都有學習過相機的內部參數和外部參數矩陣，網路上也有很多說明文章，不過在學習過程中，還是花了一些時間把一些似懂非懂的觀念釐清，所以今天想要來寫一篇文章幫大家整理最簡單的基本概念，讓學習變得更容易。

內部參數和外部參數矩陣最基本的應用就是從 2D 影像去重建 3D 世界的樣貌，也就是可以從畫面中的點去推得 3D 世界中的座標，接下來就讓我們一起來看看基本的原理。

成像的原理

最基本的相機模型，就是針孔相機。他的成像原理就是，物體反射出來的光線，透過針孔，會在針孔的感光平面上成像，如下圖所示：

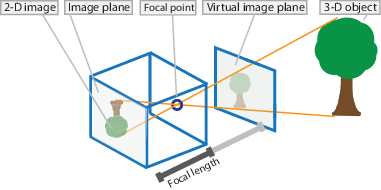
大家有時候看到內部參數的示意圖，會是如下圖：

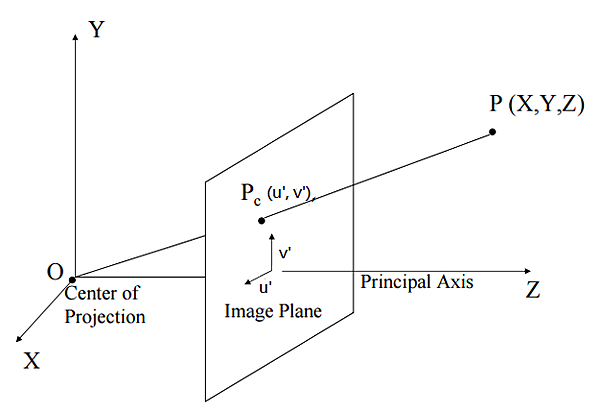
其實只是把 virtual image plane 跟 image plane 視作相同的概念，只要知道這一點，就比較不會被混淆。

內部參數矩陣

了解上面的概念之後，我們就可以利用 virtual image plane 的表示法，來幫助我們推得某一點（X, Y, Z）在 virtual image plane 上面的座標（u, v）該是多少。

首先，我們考慮最簡單的關係，

$$
\begin{bmatrix}
u \\
v

\end{bmatrix}\

\begin{bmatrix}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{bmatrix}\
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}\
$$

但是，我們的相機會因為有組裝誤差等等，不會非常理想，principal axis 不一定會落在 virtual image plane 的中心，可能會在 u 方向跟 v 方向各自有一個平移量，若這兩個平移量分別為 $t_u$ 跟 $t_v$，我們就可以將剛剛的矩陣寫成

$$
\begin{bmatrix}
u \\
v

\end{bmatrix}\

\begin{bmatrix}
f & 0 & t_u \\
0 & f & t_v \\
0 & 0 & 1
\end{bmatrix}\
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}\
$$

剛剛我們提到，目前所使用的單位還是真實世界中的單位（例如公分）。但是，在影像中的座標都是用像素的位置來呈現，所以我們希望可以將單位轉換成 pixel 數。那要怎麼換呢？其實很簡單，我們只要將所有以 cm 為單位的值，都乘上 pixel/cm（每公分有多少個 pixel），自然就可以換成 pixel 數啦。

在一般情況下，u 方向跟 v 方向的單位像素個數不會相同，所以我們就分別用 $m_u$、$m_v$ 來表示 u 方向跟 v 方向每公分有幾個像素。這樣的話，矩陣就會變成下面的形式，u、v 的單位就變成 pixel 了：

$$
\begin{bmatrix}
u \\
v

\end{bmatrix}\

\begin{bmatrix}
m_uf & 0 & m_ut_u \\
0 & m_vf & m_vt_v \\
0 & 0 & 1
\end{bmatrix}\
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}\
$$

到這邊為止，就是大家常看到的內部參數矩陣的長相。但是，如果要寫成最完整的的形式，還需要考慮 u 軸跟 v 軸不垂直的狀況，這會使得每一個像素變成一個平行四邊形，如下圖所示：

從圖中可以看到，在這個像素裡面，u 的值會隨著 v 的增加而增加，所以 u 應該要額外加上 $tan(\alpha)v$，也就會可以讓我們將矩陣寫成下面的形式：（其中 $ s = \alpha_ytan(\alpha)$）

$$
\begin{bmatrix}
u \\
v

\end{bmatrix}\

\begin{bmatrix}
m_uf & s & m_ut_u \\
0 & m_vf & m_vt_v \\
0 & 0 & 1
\end{bmatrix}\
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}\
$$

外部參數矩陣

經過上面的介紹，我們已經了解，內部參數矩陣可以幫助我們將相機座標系的某一個三維點座標投影到影像平面上的二維像素座標，但是，如果只用相機座標的話，在應用上常常會遇到一些麻煩的地方。舉例來說，如果我們現在是要用一個 camera 做 3D SLAM，在過程中，我們的相機會一直移動，這會造成我們之前已經有的某些點座標，也必須隨著相機的移動，而不斷更新。這時候，如果可以有一個世界座標系一直維持不動，就可以有一個錨定的座標系，而物體的座標點就由是藉座標系定義。

下面這張圖很清楚地可以看出外部參數矩陣的功能：

總結

用一張圖來總結，可以再將整個定位複習一次。

• 內部參數矩陣：處理相機座標系到影像座標系的投影
• 外部參數矩陣：處理世界座標系到相機座標系的座標轉換

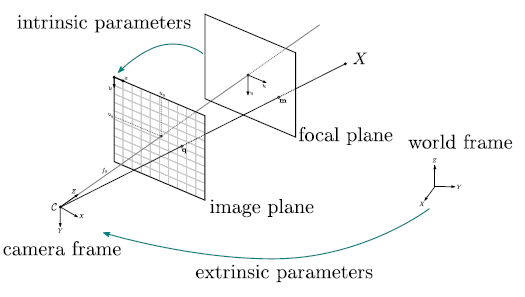
延伸閱讀

1. Pinhole Camera: 針孔相機座標成像原理
2. 計算機視覺-相機內參數和外參數
3. What Is Camera Calibration?

關於作者：

• @pojenlai 演算法工程師，對機器人、電腦視覺和人工智慧有少許研究，正在學習用心體會事物的本質跟不斷進入學生心態改進。
• @sherrychuang